Batch 3 - Class 156 - Hamiltonian Cycle Puzzles
Preclass Exercise:
- Alice and Bob are trapped by an evil logician. In their cells, Alice can see 12 trees and Bob can see 8 trees. They are told that together they see all the trees and no tree is seen by both people.
Every day, Alice is asked, "Are there 18 or 20 trees in total?" If she passes, Bob is asked the same question. If he passes too, the same process is repeated the next day.
If either ever guesses incorrectly, then both are imprisoned forever. If either guesses correctly, then both of them are released. The two can not communicate. Can they escape?
Attendance Smiti, Muskaan, Arnav, Anishka, Sanya, Gaurav, Anshi, Liza, Damini
Class puzzles
On a football, which is a regular dodecahedron in our case, we put a name of a city on each vertex. Can you go from Rio de Janeiro and go to each city exactly once before returning to Rio?
Is this always possible? For example, can you find a path in the following graph?
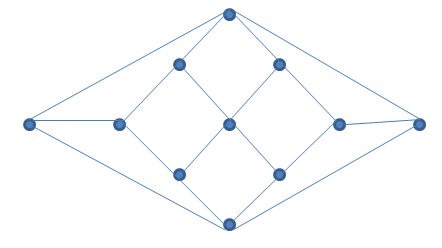
How hard is it to find this? Is there a rule (like we had in bridges of Konigsberg)?
- Finding "Hamiltonian" paths is an NP complete problem, i.e. you have to pretty much try all options and see if one works
A light bulb is connected to 3 switches, so that it lights up only when all the switches are in the proper position. But you dont know the proper position. All the switches are initially down. How many times must you press a switch, to guarantee that the light bulb will turn on?
- Answer: 7. It is the hamiltonian path through a cube as shown under
.png)
King's Frog
In the king’s miraculous gardens in Ardapasia, there is a miraculous lake on which, exactly once every year, seven miraculous lotus flowers blossom. Because they are miraculous, the lotus flowers bloom in an improbably straight and evenly spaced line, as one can see here.
The garden becomes even more miraculous when one learns of the existence of the king’s frog. When the lotuses bloom, the frog appears, as if out of nowhere, and lands on one of the flowers. The frog will then start jumping to other lotus flowers, always jumping by either three or five flowers. For instance, if the frog lands on the second lotus, then it might jump from there to the fifth or seventh lotus, and so on.
According to the customs and the everlasting tradition, the frog’s duty and privilege is to first land on a lotus from which it can embark on a journey, proceeding as indicated above, to visit each lotus once and once only. This means, of course, that the starting point and the finishing point will be different. Which lotuses can serve as starting points for the king’s frog?
- The frog can only use number 3 or 5 as starting points. To solve the problem, connect the lotuses by a line where it is 3 or 5 steps away. This will form a graph of possible movement of the frog. Now one can see that a hamiltonian path exists only from lotus 3 and 5.
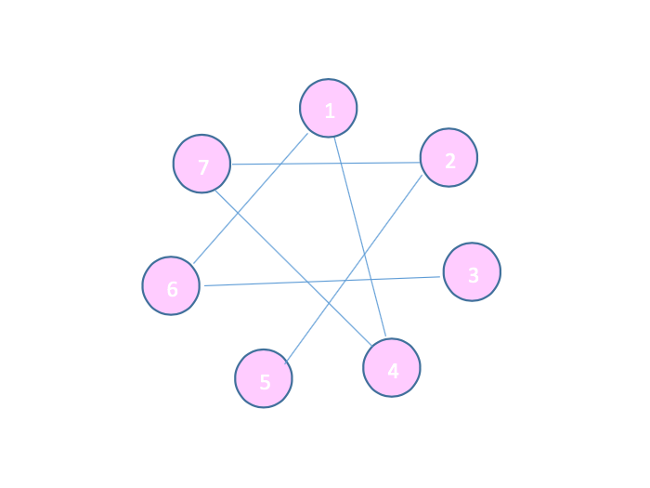
Homework Problem:
- There is a grid (lets say 3x3) of lights. Some of the lights are initially ON. Whenever you press a light, that lights and its (upto) four adjacent lights toggle. Can you switch off all the lights through this process? Example is shown below
.png)
References: